A deep dive into Starkware: blockchains, state machines, VM's, provable CPU's.

This is a branching, trademark deep-dive of mine into how Cairo and StarkNet works, when I first entered the Starknet ecosystem in April 2022. It was originally a Twitter thread which was very well-received - it got retweeted by Paradigm, and one friend of mine described it “like a mechanic stripping down a car”, which I quite liked. That being said - it was a story. I’ve rewritten it as a blog post so it’s linkable and searchable, but the order of sections has been rearranged a bit to make this more useful for people to read. I want to make this clear though - my exploration was not linear, it was long, winding, extremely fun and riveting, and this structuring is not the organic output - but a rewrite. Just like science is.

Sections:

• What is a blockchain?
  • replicated state machines
  • prover-verifier architectures and ZK
  • consensus vs. verifiability properties
  • ZK stark blockchains: O(N) vs O(log N)
• Cairo
  • High-level language - Cairo
  • Interpreted on a CPU - the Cairo CPU
  • Which creates a trace (history of CPU registers)
  • Which is compiled down to maths - Arithmetization
• Cairo explorations - word size, memory model.
  • Paradigm flip - read-only memory.
  • Asserting memory to write to it.
  • Word size - 252 bits.
• Cairo explorations - how does an ERC20 transfer look in Cairo’s CPU?
  • Syscalls - a way to write to external storage.
  • Syscalls are implemented like x86 interrupts int 80h.
  • Syscalls call builtins, which are like EVM precompiles that exist at predetermined memory addresses.
  • Writing to storage is calling a builtin, which externally is hooked by the Starknet blockchain.
  • storage_write syscall history is equivalent to EVM access lists.
• Cairo oddities - hints.
  • Back to prover-verifier architectures.
  • Computing the square root is different to verifying it.
  • Nondeterministic computation.
• StarkNet blockchain:
  • Constraints - max steps for the VM, cost of storage reads/writes.
  • Comparison to Polygon.
• The prover architecture.
  • Fact registries.
  • How do we know we are verifying a specific Cairo program?
  • Verifier contracts on Ethereum mainnet.
• Analogies to understand the Cairo stack:
  • Java -> JVM bytecode -> JVM -> x86.
  • Cairo -> Cairo bytecode -> Cairo CPU -> AIR -> Proof.
• A beautiful anecdote - science and discovery of STARK’s.

What is a blockchain?

Blockchains are cool because it’s a programmable worldwide computer (aka state machine).

A state machine is a function which transitions between two states according to some rules. In Ethereum, the state machine is the EVM. You send a transaction to a contract, the EVM loads the contract bytecode, and starts executing with the payload of msg.data. When the EVM finishes executing the tx (which probably included updating storage, balances), we get the new state of the blockchain.

How do we know nodes actually run the computations? Well, they have the incentive to do so - the block reward from producing the next block.

How do we verify blockchains aka state machines?

How do we know if the computation is run correctly? Every node verifies the transactions. A common misunderstanding - a 51% attack does NOT give you the ability to arbitrarily change balances. Nodes always verify the state transition. A consensus-level attack only changes the facts on which transactions are included in blocks (including past blocks).

So now we understand - consensus and verifiable state machines are two separate aspects of a blockchain.

The verifiability is useful, but it’s really expensive. It’s O(n) to verify a transaction, since we have to run it on our machine. Is there a shortcut?

Prover-verifier architectures.

ZK STARKS are a different model of computation, where there is a prover that tries to convince a verifier of a fact. This is a more general model of computation than a state machine, and can be cheaper too.

In EVM-land, prover and verifier both do the same thing. The prover runs the tx in the EVM, the verifier runs the tx in the EVM. It’s the same O(N) cost.

In STARK-land, the prover actually convinces the verifier using a different technique to running the whole computation.

The prover translates the computation into an equation using a technique called arithmetization.

This equation can be evaluated much more cheaply than running the whole computation. A ZK-STARK proof costs O(log^2 n) to verify.

EVM - O(n)
ZK-STARK - O(log^2 n)

Some notes here I wrote on ZK proofs back in 2018, before starkware was even out. Might be useful for beginner’s intuition.

STARK’s are a vastly better model of computation in blockchains. Optimistic Rollups only scale us linearly - they just outsource computation to a second layer, and inevitably fraud proofs do cost O(n) on layer 1.

Cairo.

So Starkware have built a VM on top of ZK-STARK proofs. Instead of writing computation in terms of equations, we can write them just like regular programs - line-by-line, w/ variables, and if statements.

That VM is called Cairo. It’s also the language.

Cairo whitepaper

This is where it starts to get confusing.

Cairo (language) compiles down to the Cairo machine bytecode, which is called AIR.

AIR stands for Algebraic Intermediate Representation - aka the arithmetization technique I was mentioning before.

The Cairo machine is an implementation of a verifier. It does not generate proofs, it merely verifies a computational trace is valid.

Provable CPU - trace.

What is a trace?

When you run a program in the Cairo CPU machine, every read/write to the CPU’s registers generates a trace.

It’s useful to think of a trace as simply a table of the CPU registers over time, where every column is a register, and every row are the values at time t.

Some example on an execution trace for encoding the computation of the Fibonacci sequence- https://medium.com/starkware/arithmetization-ii-403c3b3f4355

Cairo explorations - word size, memory model.

Coming to memory - how does the Cairo machine’s memory work?

There is a single immutable stretch of memory. Cairo instructions operate on a single cell in this memory. That cell is specified by the value in the ap/fp registers (more on this…)

So there are three registers in Cairo’s machine:

pc - program counter
ap - allocation pointer (aka free memory pointer in evm)
fp - frame pointer (used to reference the current call frame)

One thing that surprised me early on was that Cairo/Starkware allows for composable smart contracts.

This is how cross-contract calls look in Cairo VM memory-

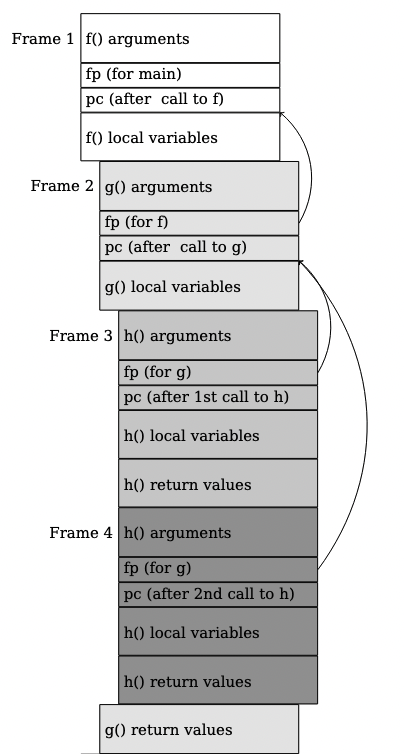
Interesting…so I’m just learning how addition/multiplication work in Cairo.

In EVM, you might push two values to the stack, and then call ADD, which puts the sum in stack position 0.

In Cairo, the word size is a felt (field element), which is 252 bits. https://cairo-lang.org/docs/hello_cairo/intro.html#the-primitive-type-field-element-felt

A Cairo instruction can span 1-2 words. Unlike other CPU architectures, Cairo instructions are packed very differently. The 1st word contains the instruction, flags and values. The 2nd word contains the input (imm - immediate value).

I’ll be honest it’s literally easier to read the state machine code than try explain this. See pg. 33

As I understand:

op1, op2 - operands
imm - immediate value
res - result
dst - destination

res/dst are used for jumps
res/dst also used for assertions

Notably missing - Cairo machine doesn’t have mstore/sstore! The machine’s memory is immutable read-only. How do they implement read/write then?

Like a simple example - an ERC20.transferFrom function. How do we update the balance of receiver?

Cairo explorations - how does an ERC20 transfer look in Cairo’s CPU?

Cairo doesn’t have the concept of storage. But StarkNet does. And what’s confusing is that you use the same language, but a different compiler (cairo-compile vs. starknet-compile)

When we think about writing to memory, we think about it happening while the program is executing. But that’s not really how our computation is running, since it’s a proof.

Instead, we use assertions to write to memory.

When we assert a memory cell is a certain value, the Cairo prover generates a trace which says that cell has a value.

That functions as an assignment. The traces are in fact a history of a program’s memory.

Assertions can literally be for any number in the field, e.g. 123123123 = 123123123

Interpreting an assertion as an assignment, where the left-hand side is the address and right-hand side is the value, we can view it as a massive address space for our program’s memory.

And just like EVM has precompiles, we can define certain areas of that address space to use for communicating with the outside world! (e.g. SSTORE). Cairo calls these builtins.

The memory model is a little more sophisticated. Basically builtins exist at predefined memory segments. The memory segments are handled by the Cairo Runner, which is the runner for your Cairo program on top of the Cairo machine (but before the Cairo bootloader).

An example of how invoking a builtin works-

Coming to some actual Cairo code to understand how this compiles down, this is an example of a token contract in .cairo-

# State.
@storage_var
func _balance(account : felt) -> (balance : felt):
end

The storage_var annotation is actually just some syntactic sugar that generates a getter/setter. It generates something like this-

# From the Starkware source code:
# https://sourcegraph.com/github.com/starkware-libs/cairo-lang@master/-/blob/src/starkware/starknet/compiler/storage_var.py?L72-95
    code = f"""\
namespace {var_name} {{
    from starkware.starknet.common.storage import normalize_address
    from starkware.starknet.common.syscalls import storage_read, storage_write
    from starkware.cairo.common.cairo_builtins import HashBuiltin
    from starkware.cairo.common.hash import hash2

    func addr{{pedersen_ptr: HashBuiltin*, range_check_ptr}}() -> (res: felt) {{
        {addr_func_body}
    }}

    func read{{
        syscall_ptr: felt*, pedersen_ptr: HashBuiltin*, range_check_ptr
    }}() {{
        {read_func_body}
    }}

    func write{{
        syscall_ptr: felt*, pedersen_ptr: HashBuiltin*, range_check_ptr
    }}(value: felt) {{
        {write_func_body}
    }}
}}\
"""

The way you write to storage looks like this-

balances.write(caller, new_balance)

But what does .write actually compile down to?

Basically .write is an autogenerated function, which writes data word-by-word into memory by calling the storage_write builtin.

# From the Starkware source code:
# https://sourcegraph.com/github.com/starkware-libs/cairo-lang@master/-/blob/src/starkware/starknet/compiler/storage_var.py?L228-233
    write_func_body = f"let (storage_addr) = addr({args});\n"
    for i in range(var_size):
        write_func_body += (
            f"storage_write(address=storage_addr + {i}, value=[cast(&value, felt) + {i}]);\n"
        )
    write_func_body += "return ();\n"

Ok so how does storage_write work?

Fun fact - all of the Cairo builtins are actually written in Cairo itself! This is actually a really good signal - decoupling/separation of concerns in the Starkware stack makes me think that they’ve designed these primitives to do one thing really well.

Here’s the storage_write builtin. It’s called a syscall here.

// From the Starkware source code:
// https://sourcegraph.com/github.com/starkware-libs/cairo-lang@master/-/blob/src/starkware/starknet/common/syscalls.cairo?L282-288

// Describes the StorageWrite system call format.
struct StorageWrite {
    selector: felt,
    address: felt,
    value: felt,
}

func storage_write{syscall_ptr: felt*}(address: felt, value: felt) {
    assert [cast(syscall_ptr, StorageWrite*)] = StorageWrite(
        selector=STORAGE_WRITE_SELECTOR, address=address, value=value
    );
    %{ syscall_handler.storage_write(segments=segments, syscall_ptr=ids.syscall_ptr) %}
    let syscall_ptr = syscall_ptr + StorageWrite.SIZE;
    return ();
}

Breaking down this function:

1. It allocates a new struct, the StorageWrite struct, which encodes the call into memory (which will generate a trace of that syscall)
2. It writes that StorageWrite to the syscall_ptr, using an assertion

Cairo syscalls seem similar to Linux interrupts (int 80h)? Write the arguments and syscall identifier to memory, and then call an interrupt opcode?

The execution trace of storage_write calls is the equivalent of Ethereum’s accessed_storage_keys (EIP-2930) (access lists).

What’s the syscall_ptr? This is what is known as an “implicit” argument that you will see EVERYWHERE in Cairo. It’s one of the ugliest parts of the language, since it needs to be mentioned anywhere you use a syscall/builtin. See the docs.

It makes sense why we need it though. The Cairo Runner presumably defines the memory segments where syscalls are to be written to (syscall_ptr), and this is passed into the user’s Cairo program when it is run. ie. syscall_ptr is dynamically injected at runtime

Cairo oddities - hints.

Okay, what about this weird line with the {% syntax? What’s that do?

%{ syscall_handler.storage_write(segments=segments, syscall_ptr=ids.syscall_ptr) %}

That is one of the weirdest parts of Cairo - Hints.

Recall back to the paradigm shift around “memory”. When we transact with a Cairo program, we actually are generating a proof of that computation being run correctly. The execution trace stores the history of the program’s memory during exec.

What I didn’t mention is that the execution of the Cairo machine can be NON DETERMINISTIC - the prover may do additional work that is not part of the proven computation. They refer to this as “nondeterministic programming”. The example they use is really terse and I love it.

The verifier doesn’t need to know how you compute the square root - only that it satisfies some relation. This opens up Cairo for some very interesting applications.

How this works - you can write anything to memory during the proof generation, and you can even do it in languages other than Cairo! The {% %} syntax lets you write to memory using Python. It will generate a trace of any modifications, just like a regular Cairo assignemnt. And when syscall_handler.storage_write is called, it routes to the StarkNet OS backend.

StarkNet blockchain.

What I don’t understand yet is how the whole thing fits together– do proofs get generated locally or server side? I imagine they get generated on the StarkWare server. But if they’re generated on Starkware’s side, where are hints evaluated?

So far, I’m reading the entire StarkNet blockchain is actually implemented in Cairo -

# From the Starkware source code:
# https://sourcegraph.com/github.com/starkware-libs/cairo-lang@b614d1867c64f3fb2cf4a4879348cfcf87c3a5a7/-/blob/src/starkware/starknet/core/os/transactions.cairo?L120-139

# Executes the transactions in the hint variable os_input.transactions.
#
# Returns:
# reserved_range_checks_end - end pointer for the reserved range checks.
# state_changes - StateChanges struct corresponding to the changes that were done by
#   the transactions.
#
# Assumptions:
#   The caller verifies that the memory range [range_check_ptr, reserved_range_checks_end)
#   corresponds to valid range check instances.
#   Note that if the assumption above does not hold it might be the case that
#   the returned range_check_ptr is smaller then reserved_range_checks_end.
func execute_transactions{
    pedersen_ptr : HashBuiltin*,
    range_check_ptr,
    ecdsa_ptr,
    bitwise_ptr,
    outputs : OsCarriedOutputs*,
}(block_context : BlockContext*) -> (reserved_range_checks_end, state_changes : StateChanges):
    alloc_locals

Looks like the StarkNet Sequencer has a whitelist of hints. I’m going to guess that when you deploy a StarkNet contract, you’re uploading the list of hints in the compiled contract .json. Somehow it figures out where hints are invoked during the program? Let’s see-

# https://sourcegraph.com/github.com/starkware-libs/cairo-lang@b614d18/-/blob/src/starkware/cairo/lang/vm/virtual_machine_base.py?L143-147
"""
        hints - a dictionary from memory addresses to an executable object.
          When the pc points to the memory address, before the execution of the instruction,
          the executable object will be run.
          Executable objects are anything that can be placed inside exec.
          For example, 'a=5', or compile('a=5').

hints : a dictionary from memory addresses to an executable object
226 is presumably the mem addr, and the exec obj is presumably the .code

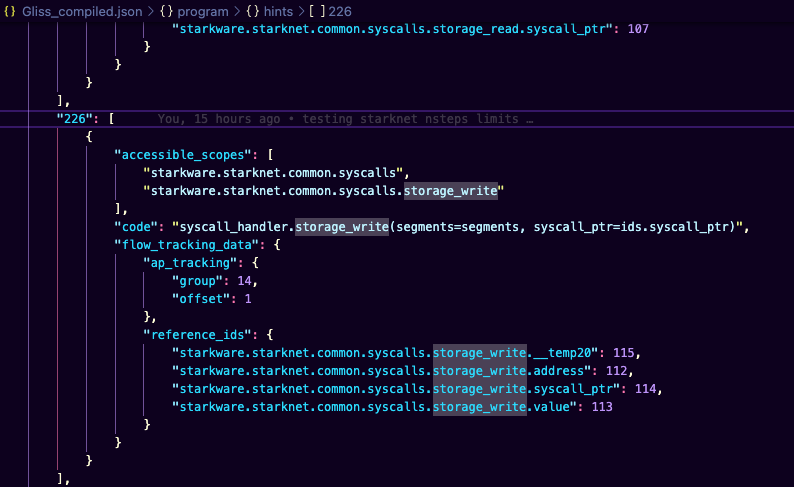
Constraints.

Constraints I’ve found on StarkNet so far:

Max Cairo machine steps - 1_000_000. [1]
Storage read/write is 40 steps [2]
So that’s max 25k r/w per tx.

# https://sourcegraph.com/github.com/starkware-libs/cairo-lang@master/-/blob/src/starkware/starknet/definitions/general_config.py?L50
# In order to be able to use Keccak builtin, which uses bitwise, which is sparse.
DEFAULT_MAX_STEPS = 10**6

# https://sourcegraph.com/github.com/starkware-libs/cairo-lang@master/-/blob/src/starkware/starknet/business_logic/execution/os_resources.json?L117-125
        "storage_read": {
            "builtin_instance_counter": {},
            "n_memory_holes": 0,
            "n_steps": 44
        },
        "storage_write": {
            "builtin_instance_counter": {},
            "n_memory_holes": 0,
            "n_steps": 46
        }

So for transferring 1M tokens at once, that would be 40 transactions worth. Not too bad. Not sure about gas costs yet.

Compared to Polygon (reference in my previous research):

Gas throughput per second (not per tx) - 9.2M
SLOAD is 20k gas
9_200_000 / 20_000 = 460

StarkNet’s looking like a 54x improvement in throughput.

It’s not ZK.

So I just realised something quite dumb. But since I’m dumb I imagine many people might think this. STARKS don’t have to be ZK. Starkware/StarkNet/Cairo are all just STARK-based. There is no private element to them (like Circom from memory).

The prover architecture.

Cairo’s prover architecture, the fact registry and the Cairo Runner-

Cairo proofs are modeled after a fact registry. A Cairo program is executed with inputs, outputting an execution trace (showing the full state of memory over time), which is reduced to a STARK proof.

The Cairo STARK proof verifies that running a program with those inputs will generate this output - this is the fact we are submitting to the fact registry. What’s the fact registry?

The fact registry is a smart contract on Ethereum Goerli, which verifies STARK proofs and stores facts that are of the form keccak(program_hash, output_hash). The current fact registry is located at 0xAB43bA48c9edF4C2C4bB01237348D1D7B28ef168.

This is a proxy pointing to a proprietary contract with the interface IFactRegistry.sol. Doing some sleuthing, you can find a couple of implementations across Starkware’s repos though that glean some more information - eg.

The fact registry isn’t a complex contract - it’s just a KV store where you can call registerFact(fact). The juice is in the Solidity STARK verifier. Here’s GpsOutputParser, which processes the output of the SHARP prover service (prev. called GPS):

// https://sourcegraph.com/github.com/starkware-libs/starkex-contracts/-/blob/evm-verifier/solidity/contracts/gps/GpsOutputParser.sol?L66
    function registerGpsFacts(
        uint256[] calldata taskMetadata,
        uint256[] memory publicMemoryPages,
        uint256 outputStartAddress
    ) internal {

The external entrypoint to proving STARK proofs on-chain is in GpsStatementVerifier.verifyProofAndRegister.

Again, I keep coming back to the Cairo paper, just so succinct. In all ZK proof systems, we have a verify(proof) function. We can verify a proof is correct, but how do we know what program it is proving? For this, there is the Cairo runner. What the runner does, is write the hash of the program and its inputs to public memory. ie. something like this-

run(program, inputs):
  write(public_mem, hash(program, inputs))
  program(inputs)

It calls out to CairoVerifier, which looks to be polymorphic, with a couple of specific implementations for different memory layouts. Interesting stuff! See starkware-libs/starkex-contracts/evm-verifier/solidity/contracts/cpu/CairoVerifierContract.sol.

Facts are of the form keccak(program_hash, output_hash), where:

• program_hash is the Pedersen hash of the compiled program, and
• output_hash is the keccak hash of the output field elements

Aha! So this explains how we know which program we are proving - we have the hash of the bytecode, as part of the fact. So we can store our Cairo CPU’s hash (they call it the Cairo bootloader) inside a verifier, for example, and then verify any proof we pass to it corresponds to the bytecode with that hash.

Analogies to understand the Cairo stack.

Honestly if I were wanting to get a young student into maths, comsci and software, I’d get them to read the Cairo paper. It’s 22 pages of some of the most interesting and concise explanations of computer science topics I’ve ever read. It’s beautiful.

It goes from “computation can be represented as y=mx+c” to “let’s design a CPU, instruction set and high-level programming language”

And it’s just so freaking interesting. A paper where they build a CPU, instruction set, memory model, program runtime, and programming language. All justified within the constraints of arithmetic on prime numbers (field elements). (note on republishing this in June 2023, I realise that the field operations are not in fact prime numbers. However, the analogy for noobs is more useful - ZK-S[NT]ARKS rely on similar cryptographic assumptions to asymmetric public key crypto, so it’s relatively easier to grasp that the numbers we use are in the same league as primes, without talking about discrete log assumptions and other stuff).

AIR = assembly for STARK’s
Cairo = C for STARK’s
Prover = gcc/clang

(easy mental shortcuts to explain this)

Okay Cairo is maybe a bit more than just “C for STARK’s”. It’s more like Java. (thanks @GuthL for clarifying this for me!)

.cairo -> cairo VM bytecode
.java -> JVM bytecode

JVM bytecode is interpreted into assembly.
Cairo bytecode is interpreted into AIR.

So like:

java -> JVM bytecode -> assembly -> x86
cairo -> Cairo VM bytecode -> AIR

x86 runs on Intel CPU’s
AIR runs inside a STARK prover like Winterfell

A beautiful anecdote - science and discovery.

What’s seemingly beautiful about the invention of SNARK’s is that it was truly also a process of discovery.

I didn’t realise this, but they had to literally search for the parameters of two elliptic curves - MNT4 and MNT6 - which took over 610,000 compute hours.

Epilogue.

Writing is both an instrument for communicating information as well as thinking itself. Just like an LLM, we have limited memory and writing can help us with that. The Cairo whitepaper is the best paper I have ever read, and the teams working on it some of the smartest engineers I’ve ever come across.

I commenced this deepdive because I wanted to build an on-chain social network where attention is tokenised. Your influence would thus be an aggregate of all the attention people paid you. And you could build influence markets, and other interesting mechanisms. Unfortunately, this idea was impossible in current blockchains - for a user with 10,000 followers, selling their influence would involve atomically selling 10,000 different tokens. Current EVM chains (Polygon) have a max tx gas limit of 5M gas, which would cap this out around ~500 different token sales. And so I persisted on, deeply curious.

I know STARK’s had some interesting properties, so I reached out to Starkware and started asking questions. Within 2hrs I was on the phone to a lovely French guy named Louis - (in a deep french accent) ok so what I am going to do, is give you a grant I was set. From that moment, I just dived in and started reading/writing. It turns out the StarkNet step limit was too low to achieve even what I wanted to, so I just started reading about Google Bigtable and how you could parallelise stuff. This is what led me to reading about and understanding the potential of recursive ZK proofs - aka verify a proof within a proof. There is an architecture we can build which is a blockchain with a horizontally-scalable storage backend. I did some research on acheiving this, based on Google’s Bigtable database here. If you’re interested in this or anything else, please reach out. It’s still an open problem that I’d love to solve.

Many thanks to Starkware and the community for their ongoing vibes. You guys are awesome.