I learnt a new term for an intuition I've developed for a couple different problems recently called the kernel method (or trick, method sounds more philosophical).
Firstly, some background: one of my hobbie projects right now is applying the hallmark algorithm behind Google to the abstract syntax tree's of codebases.
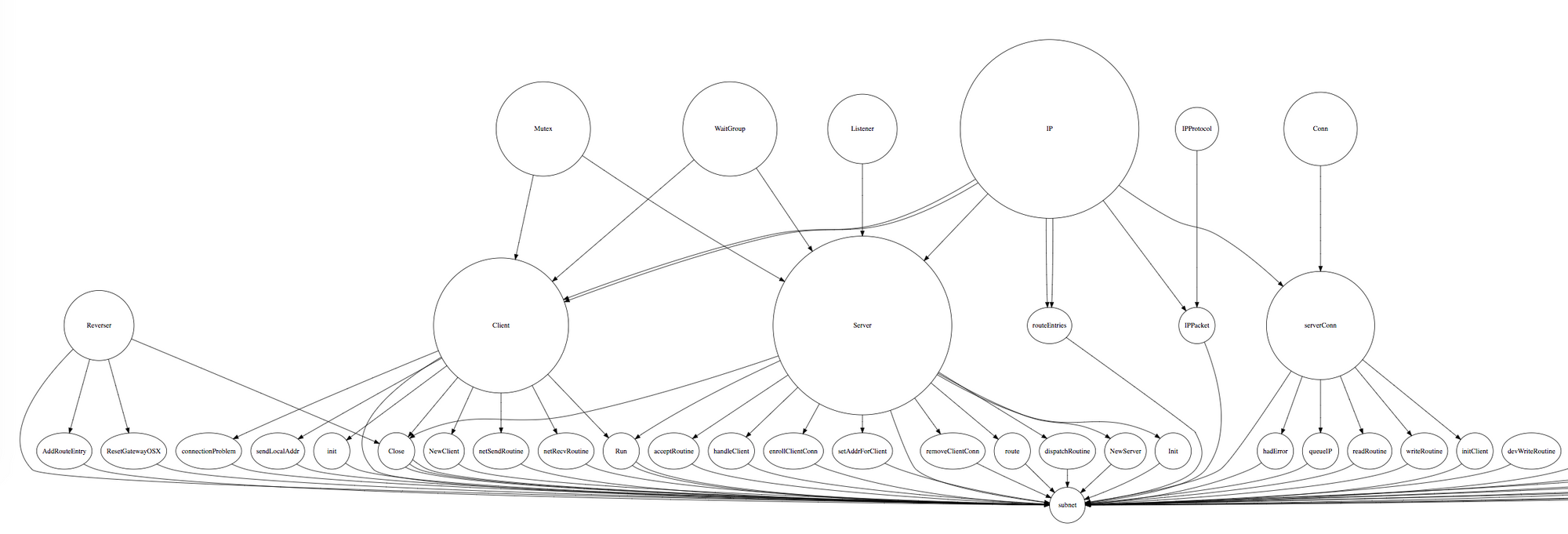
Here's what a visualisation looks like currently:
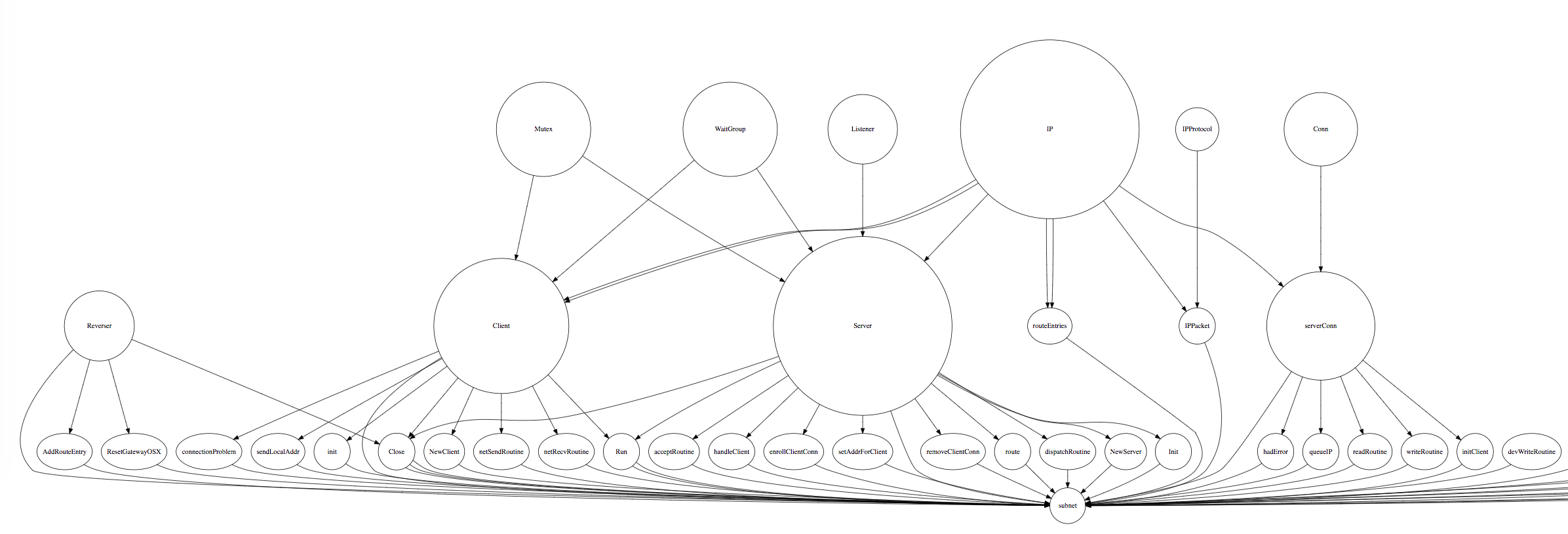
which is generated from files like this:
I want to see how well it models the important parts of the codebase. Only pursuing it out of intellectual curiosity for now, but it definitely paints a nice picture of my friend's minimal Go VPN for someone new to it.
The algorithm is very simple:
- Parse code, build AST
- Recurse AST, build graph from links between identifiers
- Run PageRank to calculate each identifier's importance
Step #2 looks like this:
The beauty of it vests in PageRank's versatility in determining how important a node is. In more general terms, we could say PageRank is extracting a feature called importance for every node in the codebase (where a node is an identifier such as for a type, function, argument). The interesting aspect being that the data it's given is simply identifiers and their usages; nodes and edges of a graph.
PageRank
The PageRank algorithm determines a webpage's importance by the importance of sites linking in to it, which is moderated by how many outbound links they make. Very similar to being friends with a celebrity and thus being more famous yourself, except if everyone is friends with Bob Marley then saying you knew him is less impressive than saying you smoked up with Satoshi Nakamoto.
The other aspect to PageRank is a damping factor \(d\), which simply means as a web surfer you don't have all day to spend on the Internet, and likewise not enough time to maintain relationships with everyone in Madagascar (at least, not with that attitude).
So for any node \(N_i\) and its inbound links \(I\) in a graph of \(\boldsymbol{n}(N)\) nodes, the PageRank \(PR\) is:
$$PR(N_i) = \frac{1 - d}{\boldsymbol{n}(N)} + d \sum_{n \in I_n} \frac{PR(n)}{\boldsymbol{n}(I_n)}$$
Although the definition is recursive, it can be algebraically represented and iteratively computed (indeed, Google does it batchwise).
Teaching old DAG's, new (kernel) tricks
The salient characteristic of PageRank, and many other successful machine learning algorithms, is that we define how it computes features only from relative measures. In PageRank's case, I'm referring to the 'recursive' nature of its definition; defining a page's importance is based in the importance of the pages that link to it [^1: Although I'll note that PageRank diverges a bit from this definition. Note that the non-recursive variables are the total number of nodes and the damping factor, so it is defined on the graph itself, if you consider its general definition.].
In computer vision
I built an image alignment algorithm this semester for aligning thermographic images of breasts (for cancer detection). Using an algorithm extracting descriptors of features, we detected the location of nipples throughout a whole dataset of images. Instead of manually engineering a kernel for checking for the nipple, we can use SIFT to construct a representation automatically. Where this kernel is relatively defined, is that it doesn't measure the skin colour of the pixels or the circular shape, but how each pixel's colour changes relative to each pixel surrounding it, and the gradient and magnitude of this change (such that you get an orientation). Here's a visualisation of what these gradients represent:
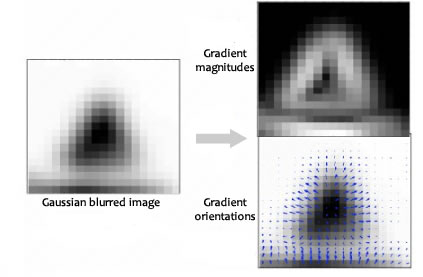
So instead of calculating the exact feature itself using a manually-engineered kernel, we calculate a distance of that datum from another datum using a kernel function and use this intra-feature distance as the feature. [^There's a link to hash functions and blockchains here, I'm sure...😉].
Conclusion
And so this is called the kernel trick, as instead of defining a kernel, we define a kernel function that "enables them to operate in a high-dimensional, implicit feature space" simply by nature of relative intuition. Sounds like my life in general!